擺脫挫折的統計學入門

前言

第一部 數學準備篇
第一章 數學不是「UNO」，而是「Pageone」
1.1 數學不是「UNO」，而是「Pageone」
1.2 數學書的閱讀方式：數學家也不可能一目十行
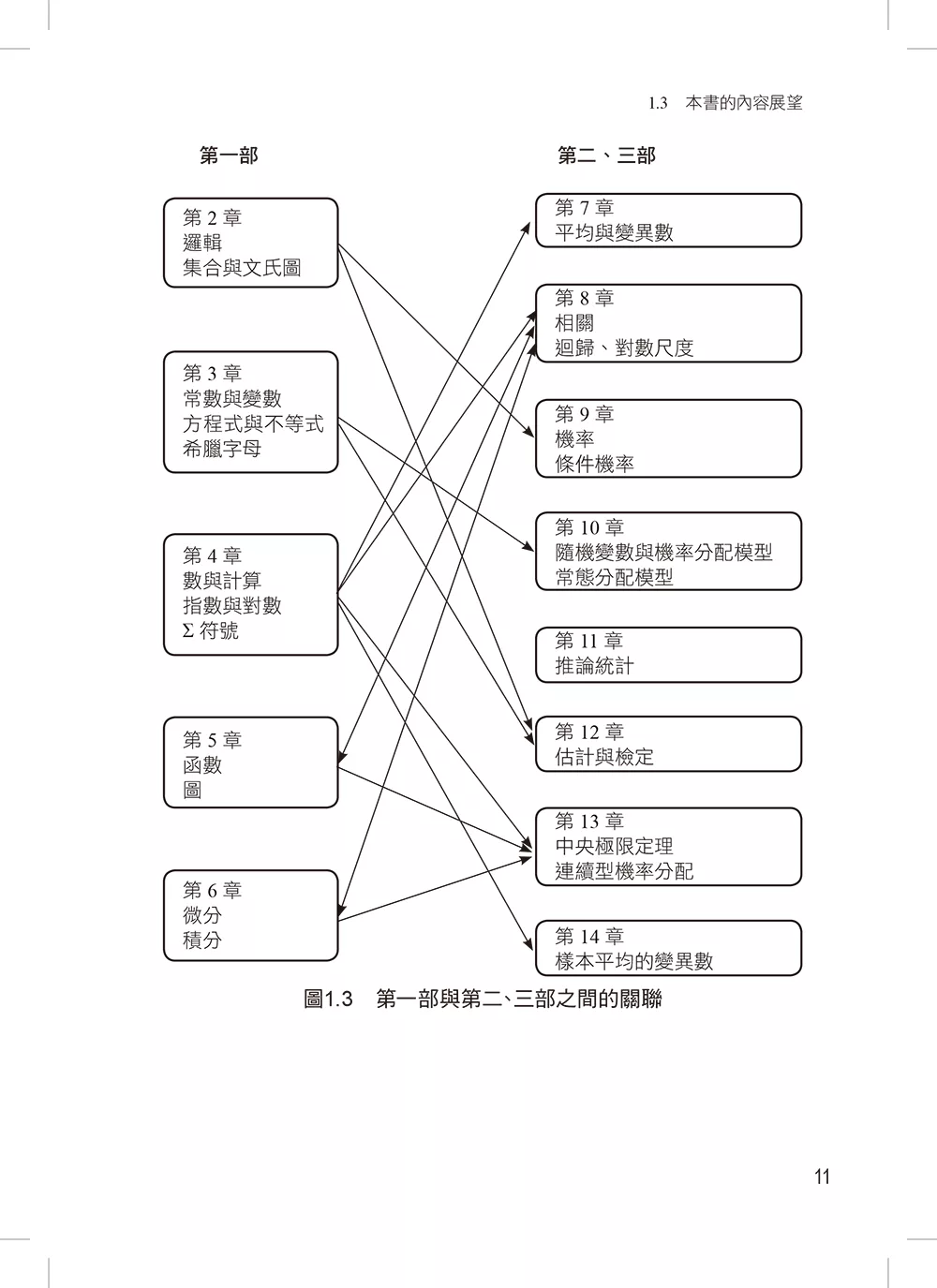
1.3 本書的內容展望

第二章 狡猾的政客
2.1 狡猾的政客，會做出「可以實現的承諾嗎」？
2.2 「數學的邏輯」與「科學的態度」
2.3 邏輯與集合
2.4 回過頭來看「我不會做出無法實現的承諾」的意義

第三章 希臘字母看起來好帥
3.1 數學與數學式內的字母：變數與常數
3.2 「=（等號）」的各種意思
3.3 等號與方程式
3.4 不等號與不等式
3.5 為什麼要用希臘字母呢？

第四章 加法→乘法→次方，逐漸演進的計算方法
4.1 計算方式的發展
4.2 逆運算與平方根
4.3 指數的推廣
4.4 對數
4.5 符號Σ表示「把n個數加總」的意思

第五章 函數與數學式
5.1 以數學式表示函數
5.2 自變數與依變數
5.3 有名字的函數
5.4 畫出函數的圖
5.5 統計學與函數

第六章 從單位到微分、從合計到積分
6.1 「單位量」與「合計量」常讓人搞混
6.2 從單位到微分
6.3 從合計到積分
6.4 關於機率密度

第二部 統計學基礎篇
第七章 資料的分配、平均、變異數
7.1 統計學與屬量資料
7.2 「分散的資料」、「資料分配」
7.3 次數分配
7.4 直方圖
7.5 為什麼要取「平均」？各式各樣的平均
7.5.1 算術平均
7.5.2 幾何平均
7.5.3 調和平均
7.5.4 中位數
7.6 變異數
7.7 計算變異數時，為什麼要把數值平方呢？

第八章 相關、迴歸、決定係數
8.1 相關關係與相關係數
8.1.1 多變量分析與相關關係
8.1.2 散布圖
8.1.3 共變異數與相關係數
8.2 迴歸分析
8.3 決定係數：可以決定什麼呢？
8.4 為了求出迴歸直線
8.4.1 微分與極值
8.4.2 最小平方法與偏微分
8.5 補充：推導數學式
8.5.1 對最小平方法的數學式偏微分，推導出迴歸係數（式（8.3））
8.5.2 殘差與相關係數（式（8.5））

第九章 機率
9.1 為什麼統計的書會提到機率呢？
9.2 機率與「佔比」
9.2.1 由次數定義機率
9.2.2 拉普拉斯的定義
9.3 條件機率與「獨立」
9.4 機率的三大誤解
9.4.1 「誤以為獨立」
9.4.2 「誤以為機率相等」
9.4.3 「誤以為成本相同」

第十章 隨機變數與機率分配模型
10.1 隨機變數的概念
10.2 機率分配模型與常態分配、中央極限定理
10.2.1 機率分配模型
10.2.2 常態分配模型與中央極限定理
10.2.3 常態分配模型的性質

第三部 統計學進階篇
第十一章 推論統計與大數法則
11.1 推論統計是在做什麼呢？
11.2 次數分配與樣本的機率分配
11.3 大數法則，「通常」與「幾乎」
11.4 大數法則與保險
11.5 母體與樣本

第十二章 區間估計與檢定
12.1 區間估計
12.1.1 什麼是區間估計
12.1.2 常態分配與區間估計
12.1.3 信心水準與信賴區間的注意事項
12.2 不偏變異數、t分配與區間估計
12.2.1 不偏變異數
12.2.2 t分配與區間估計
12.3 檢定是「在某條件下的審判」
12.3.1 什麼是假說檢定
12.3.2 t分配與檢定
12.3.3 檢定的用語
12.3.4 雙尾檢定與單尾檢定
12.3.5 無法拒絕虛無假說的時候
12.3.6 關於顯著水準
12.3.7 「（在母體為常態分配，且顯著水準為5%的條件下）你在騙人」

第十三章 連續型機率分配與中央極限定理的意義
13.1 連續型機率分配
13.2 中央極限定理的意義
13.3 常態分配在現實中存在嗎？

第十四章 樣本平均的變異數：為什麼會是「樣本大小分之一」呢？
14.1 關於樣本平均的期望值與變異數
14.2 邊際機率分配與聯合機率分配
14.3 計算樣本平均的期望值與變異數的數學式
14.3.1 隨機變數的期望值
14.3.2 隨機變數之常數倍的期望值、隨機變數之和的期望值
14.3.3 隨機變數的變異數
14.3.4 隨機變數之常數倍的變異數、隨機變數之和的變異數
附錄 本書所使用的常態分配表與t分配表
索引
 

前言

　　感謝你拿起本書。

　　對我來說，在大學部工學部（大學理工學院）念書，已經是三十年前的事了，那時我們的必修課程中並沒有統計學。不過，現在的電腦與網路科技比那時還要發達許多，蒐集、處理大規模資料已是再尋常不過的事，使統計學成為一門應用廣泛的學問。最近很流行的「人工智慧」，也是在蒐集了非常龐大的資料以後，從中找出我們想要的答案，這可說是統計學發展的結晶。另外，許多大學的共同課程中，也加入統計學課程。不管學生是文組還是理組、主修哪個領域，統計學都成為了一門必備的學問。

　　若我開的統計課上有許多來自各個領域的學生，我除了教他們統計學的計算過程，也會說明「統計學為什麼要這樣計算、有什麼目的」，也就是「統計學的內在」。

　　「統計學的內在」可以用數學表示。在我開的課中，為了讓學生不要被嚇跑，我一定會在一開始就說「統計學會用到的計算只有+、-、×、÷、平方根，還有次方這六種而已喔」。但當我們開始計算平均值，用到Σ這個符號（計算總和）時，就有學生撐不下去了。遺憾的是，這樣的學生還不算少。

　　這些地方之所以會成為學生的障礙，並不是因為學生們數學差。只是因為他們並不曉得這些符號在數學領域中的使用方式，或者說他們不了解數學的「語言」，也可能只是他們剛好忘了這些符號怎麼用而已。這些學生們就因為這樣而失去了接觸統計學的機會，我覺得是一件很可惜的事。

　　因此，在開始學習「統計的內在」前，本書準備了「數學準備篇」這個章節，以說明「數學的內在」。在這個部分中，我們會先從「如何閱讀數學相關書籍」開始說明，像是數學邏輯與日常邏輯有什麼不同、變數與常數，以及數學中常用到的「希臘字母」。此外，還會提到次方、平方根、以及Σ符號等，只在數學中出現的表現方式，也會說明微分、積分的概念。

　　在做完這些數學熱身運動後，就可進入「統計學基礎篇」，開始說明統計學的基礎原理。我們會先說明在蒐集資料之後如何進行分析，也就是所謂的「敘述統計學」。不論資料大小，我們都可以用代表值、相關、迴歸等概念說明資料的特性，我希望讀者在讀過這個部分「不只能說出每一筆資料各有不同，還能夠說出資料的組成特性」。

　　熟悉以上內容之後，就可進入「統計學進階篇」。我們會學到如何從蒐集到的資料，分析未能蒐集到的資料，也就是所謂的「推論統計」。在這個部分中，「機率」扮演著很重要的角色。推論統計方法中，若知道蒐集到之資料的「組成特性」，就可以知道除此之外的資料可能會長什麼樣子，這就是這個部分的重點。

　　在這裡有一個小小的要求想要拜託準備要閱讀這本書的你，當你在閱讀本書時，如果覺得好像有掌握到某些「統計學的內在」，請你一定要試著用個人電腦跑跑看資料處理。能夠進行資料處理的工具包括Excel之類的試算表軟體，以及R這類免費統計分析軟體，市面上有相當多這些軟體的解說書籍。如果在你親手操作這些工具、處理資料時，真正意會到「這個步驟想做什麼」，才表示這些統計學的「核心」真的有成為你的一部分。

　　執筆本書時，Ohm社書籍編輯部門的各位給予我許多協助，並提供了許多很棒的建議，在此表示我的謝意。
另外，由於我申請到了平成二十八年度關西大學研修員的身分，獲得了研修費，使我能夠在這段期間內專心於研究、寫作活動。本書的部分內容也是在這段期間內完成的。

　　筆者在大學開的統計學課程中所使用的投影片已公開於網站上，網址為：racco.mikeneko.jp/Kougi/。